Introduction - Exercise i.6 A Custom Distribution of Random Numbers

Use a custom probability distribution to vary the size of a step taken by the random walker. The step size can be determined by influencing the range of values picked. Can you map the probability exponentially—i.e. making the likelihood that a value is picked equal to the value squared?

The previous random walker exercise also had varying step sizes, so I’ll start there.

In Processing

I lifted the code for my Gaussian random walker from before, then tweaked it to have the step() function again. This meant adding new next_x and next_y member variables to the class, because I like it drawing lines between the points. I also updated the example code because it looked nicer having step sizes picked from between -20 and 20 pixels.

I realised, in hindsight, I could have updated x and y positions with separate random numbers for the Guassian walker, too. That would also have given the spidery diagonal lines this one shows. I might try that later on…

My solution involving exponential probablities came out like this:

import java.util.Random;

class Walker {
  int prev_x, next_x;
  int prev_y, next_y;
  Random generator;

  Walker( Random gen ) {
    prev_x = width/2;
    prev_y = height/2;
    generator = gen;
  }

  void display() {
    stroke(0);
    line(prev_x, prev_y, next_x, next_y );

    prev_x = next_x;
    prev_y = next_y;
  }

  void step() {
    int max = 20;

    float stepsize = pickRandomFromExponentialDistribution( max );
    float stepx = random(-stepsize,stepsize);
    float stepy = random(-stepsize,stepsize);

    next_x = prev_x + (int) stepx;
    next_y = prev_y + (int) stepy;
  }

  float pickRandomFromExponentialDistribution( int max ) {
    while( true ) {
      float r1 = random(0, max);
      float r1squared = r1 * r1;
      float r2 = random(0, max);
      float r2squared = r2 * r2;

      if( r2squared < r1squared ) return r1;
    }
  }
}

Walker w;

void setup() {
  size( 640, 360 );
  w = new Walker( new Random() );
  background(255);
}

void draw() {
  w.step();
  w.display();
}

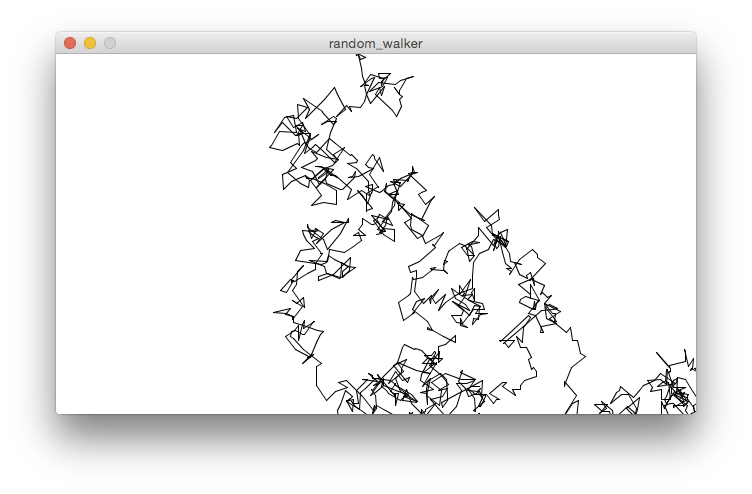
It’s based on the Monte Carlo algorithm suggested in the book. I’m not certain my algorithm is correct: I reasoned that I had to square r2 else it would be below the square of r1 disproportionately often.

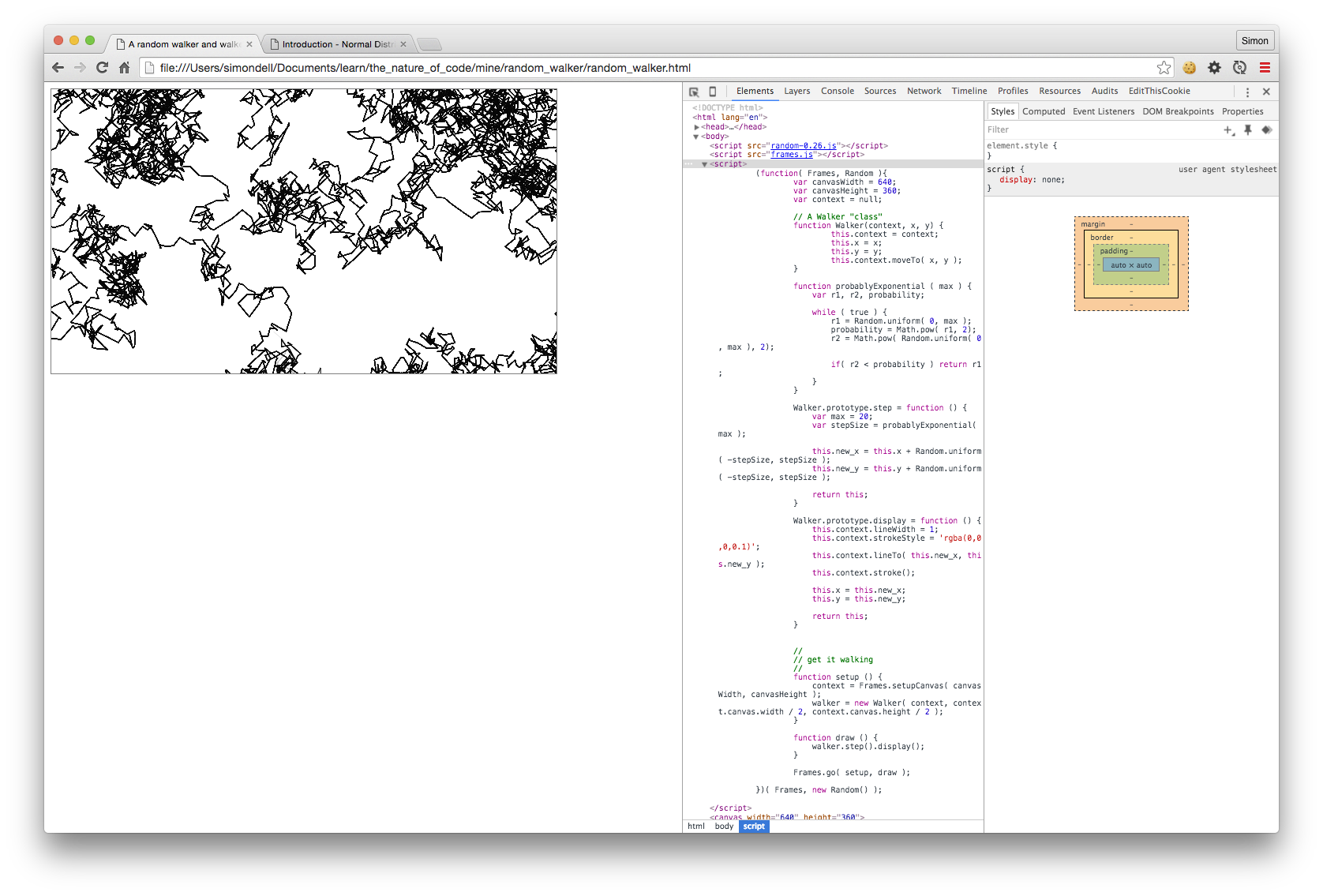
The results look similar to, but more sparse than in the linear probability provided in the exercise code. They also move off the canvas sooner (although that’s hard to show in a static screen shot). I think these characteristics are to be expected: step sizes should tend towards the larger end of the range because the probably a size will be chosen increases with its square.

In JavaScript

The JavaScript implementation is more-or-less a straight copy.

var canvasWidth = 640;
var canvasHeight = 360;
var context = null;

// A Walker "class"
function probablyExponential ( max ) {
	var r1, r2, probability;

	while ( true ) {
		r1 = Random.uniform( 0, max );
		probability = Math.pow( r1, 2);
		r2 = Math.pow( Random.uniform( 0, max ), 2);

		if( r2 < probability ) return r1;
	}
}

function Walker(context, x, y) {
		this.context = context;
		this.x = x;
		this.y = y;
		this.context.moveTo( x, y );
}

Walker.prototype.step = function () {
	var max = 20;
	var stepSize = probablyExponential( max );

	this.new_x = this.x + Random.uniform( -stepSize, stepSize );
	this.new_y = this.y + Random.uniform( -stepSize, stepSize );

	return this;
}

Walker.prototype.display = function () {
	this.context.lineWidth = 1;
	this.context.strokeStyle = 'rgba(0,0,0,0.1)';
	this.context.lineTo( this.new_x, this.new_y );
	this.context.stroke();

	this.x = this.new_x;
	this.y = this.new_y;

	return this;
}


//
// get it walking
//
function setup () {
	context = Frames.setupCanvas( canvasWidth, canvasHeight );
	walker = new Walker( context, context.canvas.width / 2, context.canvas.height / 2 );
}

function draw () {
	walker.step().display();
}

Frames.go( setup, draw );