Introduction - Exercise i.7 Walking (randomly) in Perlin's steps

Create a random walker where you map the result of the noise() function to a Walker’s step size.

In Processing

This implementation was reasonably simple as the noise() function is provided by Processing out of the box, and the tutorial had already explained how to use it.

Rather than re-use the previous random walker, I took a tip from the circle-drawing code from the last example before the exercise. This walker draws a circle rather than a dot, so the trail left is really obvious.

class Walker {
  float x,y, step_x, step_y;

  float tx,ty;

  Walker() {
    x = width / 2;
    y = height / 2;
    tx = 0;
    ty = 10000;
  }

  void display() {
    ellipse(x,y,16,16);
  }

  void step() {
    step_x = map(noise(tx), 0, 1, -8, 8);
    step_y = map(noise(ty), 0, 1, -8, 8);

    x += step_x;
    y += step_y;
    tx += 0.01;
    ty += 0.01;
  }
}

Walker w;

void setup() {
  background(255);
  size( 640, 360 );
  w = new Walker();
}

void draw() {
  w.step();
  w.display();
}

Changing the step size along the noise’ x- and y- axes changed how often the trail changed direction (as a side effect of making the step-size random).

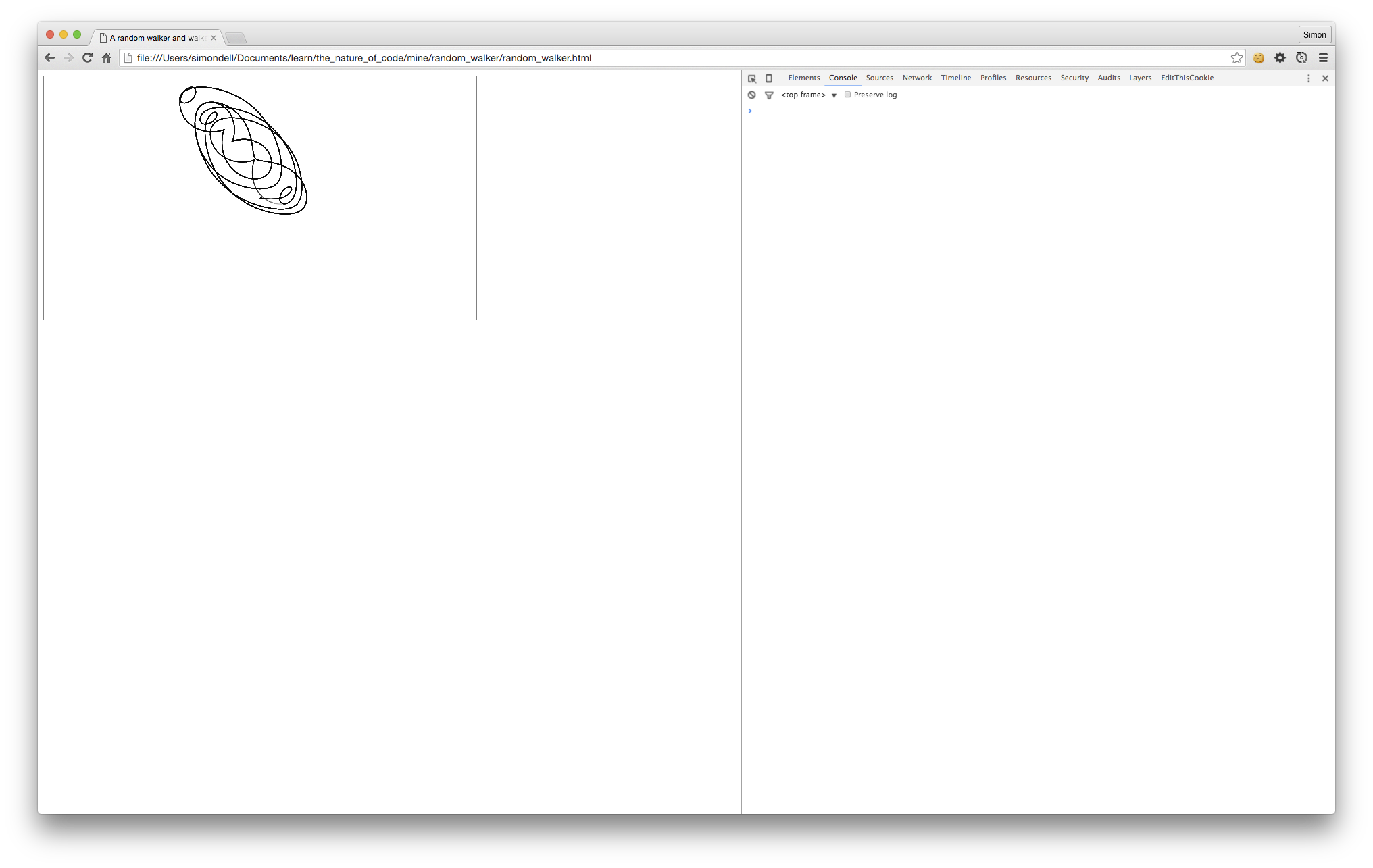
The step at 0.01 (as per the examples given), the image came out looking kind of like tentacles:

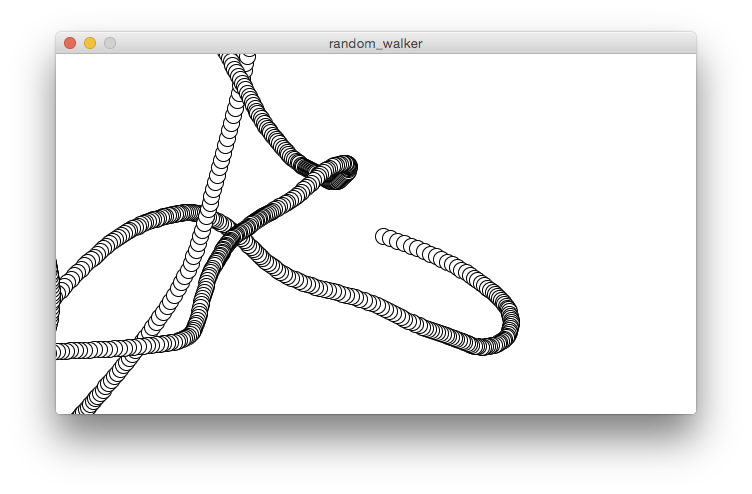
With the step at 0.05, it was more “worm-like”:

In JavaScript

The JavaScript implementation was more complicated.

I decided to stop using my Frames micro-library, because it didn’t solve any important problems useful in learning Canvas or general animation with JavaScript. It was an interesting diversion and got me thinking a little about how to create library code, but I don’t think I’ve learned enough about using canvas yet to appreciate what a library should abstract away (if anything).

Next, I needed an equivalent to Processing’s map() function. I find the name confusing, because it doesn’t do the same as map() from the functional programming paradigm. I’m not a full-time functional programmer, but I like the patterns I’ve learned so far and would rather reserve those names. Mine will have a different name. I thought I knew how to do the maths for converting a point in one range to a point in another, but after some trial and many errors I realised I didn’t. I found a couple of possible candidates on NPM, but I’m not using a build pipeline that lets me use node modules in a browser and didn’t want to create one yet. Looking into them, “map-range” was a bit too abstract for my needs but “fit-range” had just the interface I was hoping for. I delved into its code. A comment there lead me to a discussion on StackOverflow about the maths behind mapping to ranges, so I have implemented my own version based on that discussion.

function mapToRange ( num, inputMin, inputMax, outputMin, outputMax ) {
	// thanks SO: http://stackoverflow.com/questions/929103/convert-a-number-range-to-another-range-maintaining-ratio
	var inputRange = inputMax - inputMin;
	var outputRange = outputMax - outputMin;

	if( inputRange === 0 ) throw 'Input range = 0';
	if( outputRange === 0 ) throw 'Ouput range = 0';
	if( num < inputMin || num > inputMax ) throw new RangeError( 'Num is outside of input range.' );

	return ( ( ( num - inputMin ) * outputRange ) / inputRange ) + outputMin ;
}

JavaScript doesn’t provide a Perlin Noise function as standard so, just as with the Gaussian random distribution before, I needed to find a third-party implementation. Some Googling turned up this version from Kas Thomas, allegedly a port of the canonical Java code from a book by Perlin himself. Thomas’ function was provided in JavaScript but his example usage suggestions were given in pseudo-code, so I felt I should create an implementation of that before trying to follow the exercise from the book.

var canvasWidth = 640;
var canvasHeight = 360;
var canvas = document.createElement( 'canvas' );
var context = null;

canvas.width = canvasWidth;
canvas.height = canvasHeight;
document.body.appendChild( canvas );

context = canvas.getContext( '2d' );

var size = 10;  // pick a scaling value
var z = 1.6;

var step_x, step_y, x, y, n, colour;

for( step_y = 0; step_y < canvas.height; step_y++ ){
	for( step_x = 0; step_x < canvas.width; step_x++ ){
		x = step_x / canvas.width;
		y = step_y / canvas.height;
		n = PerlinNoise.noise( size*x, size*y, z );
		colour = Math.round( 360 * n );
		context.fillStyle = 'hsl(' + colour + ',' + '40%,' + '50%)';
		context.fillRect( step_x, step_y, 1, 1 );
	}
}

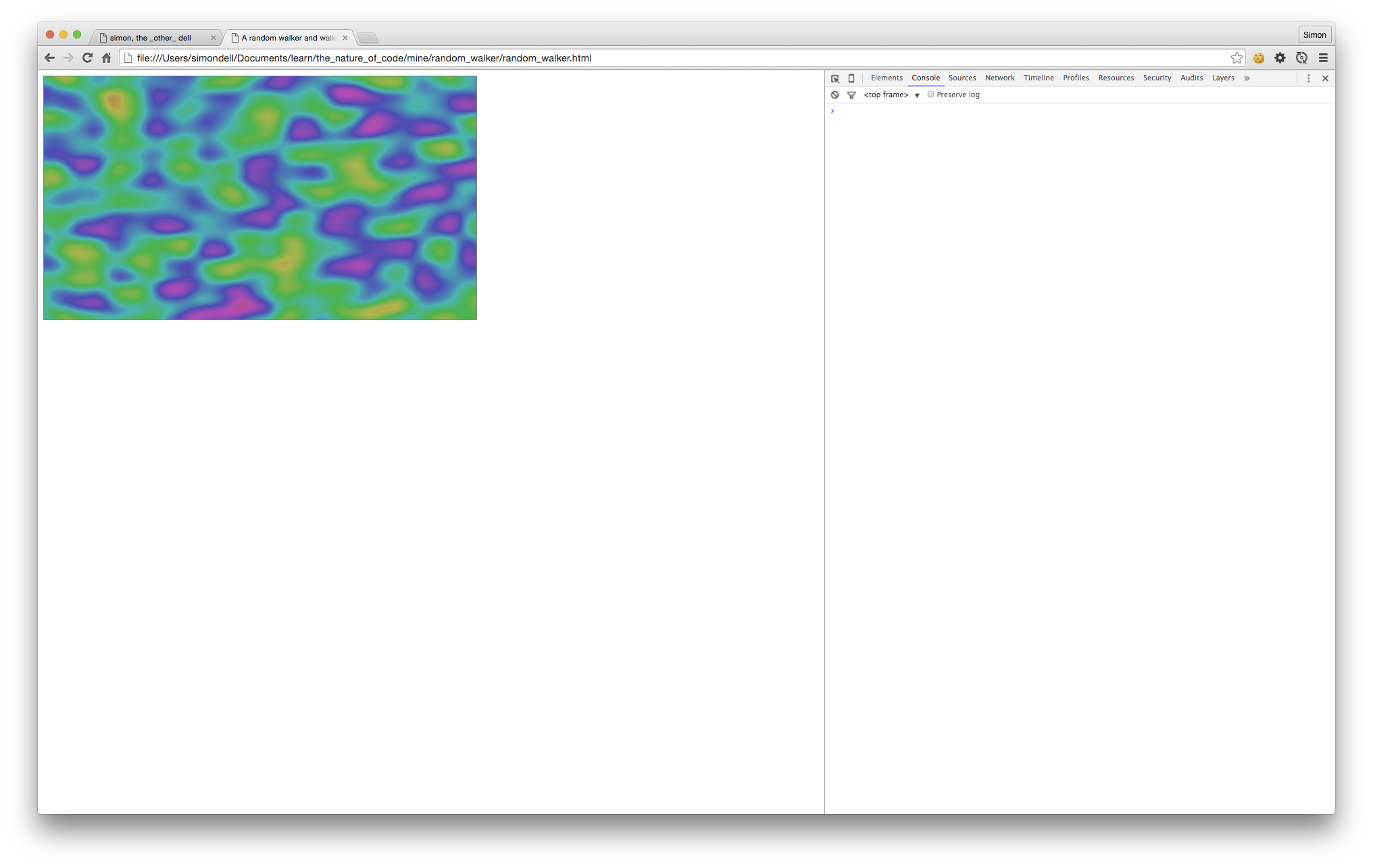
This draws a colourful, watery smudge:

When I tried to use this with a simple random walker, I found the code would hang, or throw an error to the console. At one point it managed to consume so many resources the computer locked up. For an algorithm that was designed to be fast in 1982, this struck me as “amusing”. I decided to look for another Perlin noise implementation. There [are][] (and that last link points to more, with comparisons).

I tried this one next. The library provides 2d and 3d Perlin Noise functions and also 2d and 3d Simplex Noise functions. Simplex seems to be a newer, faster, noise function capable of creating noise in more dimensions, also by Ken Perlin.

The input to the function seems to need to be between -1 and 1, and the output will be in the same range. Going outside that input range caused errors to the thrown.

(function( noise ){
	var canvas;
	var canvasWidth = 640;
	var canvasHeight = 360;
	var context = null;

	// A Walker "class"
	function Walker(context, x, y) {
		this.context = context;
		this.x = x;
		this.y = y;
		this.tx = Math.random();
		this.ty = Math.random();
	}

	Walker.prototype.step = function () {
		var t = 0.03
		var perlin_x = noise.perlin2( this.tx, t );
		var perlin_y = noise.perlin2( this.ty, t );

		var stepX = mapToRange( perlin_x, -1, 1, -10, 10 );
		var stepY = mapToRange( perlin_y, -1, 1, -10, 10 );

		this.new_x = this.x + stepX;
		this.new_y = this.y + stepY;
		this.tx += 0.02;
		this.ty += 0.02;

		return this;
	}

	Walker.prototype.display = function () {
		this.context.lineWidth = 1;
		this.context.strokeStyle = 'rgba(0,0,0,0.1)';
		this.context.moveTo( this.x, this.y );
		this.context.lineTo( this.new_x, this.new_y );
		this.context.stroke();

		this.x = this.new_x;
		this.y = this.new_y;

		return this;
	}


	//
	// get it walking
	//
	canvas = document.createElement( 'canvas' );
	canvas.width = canvasWidth;
	canvas.height = canvasHeight;
	document.body.appendChild( canvas );

	noise.seed(Math.random());

	context = canvas.getContext( '2d' );
	walker = new Walker( context, canvasWidth / 2, canvasHeight / 2 );

	requestAnimationFrame( function draw () {
		walker.step().display();
		requestAnimationFrame( draw );
	});
})( noise );

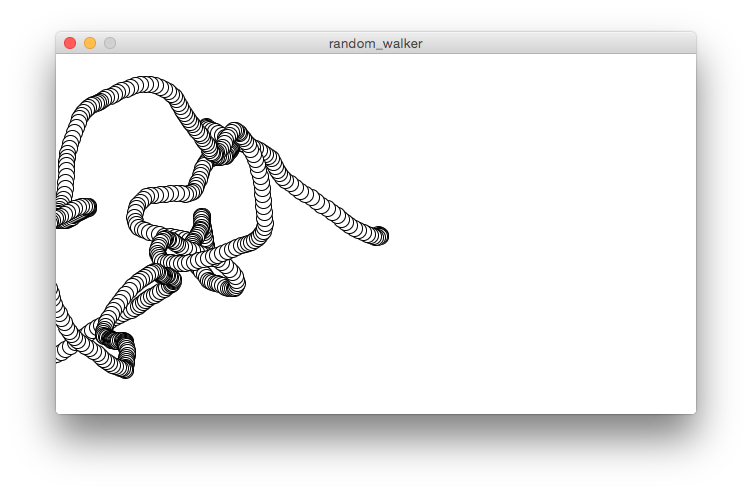
I tried a few different values for the step size along the x and y “time” axes; 0.02 was my favorite, yielding wide, looped designs like the image below.