Introduction - Normal Distribution of Random Numbers pt 3 - Gaussian Random Walker
A Gaussian random walk is defined as one in which the step size (how far the object moves in a given direction) is generated with a normal distribution. Implement this variation of our random walk
The step size in previous random walk examples and exercises was just 1. Although some of the earlier example code shows random walkers that could walk in any direction, the exercises focused on those which could walk only the four cardinal directions. My trigonometry is very rusty (and I know that the next chapter is going to go through vectors and probably some basic trigonometry to go with it), so I’m going to stick with the simpler set of choices.
In Processing
A scatter of points
Here’s my first solution:
import java.util.Random;
class Walker {
int x;
int y;
Random generator;
Walker( Random gen ) {
x = width/2;
y = height/2;
generator = gen;
}
void display() {
stroke(0);
point(x,y);
}
void step() {
float stepSize = (float) generator.nextGaussian();
int choice = int(random(4));
int mean = 10;
int sd = 3;
float distance = sd * stepSize + mean;
if (choice == 0) {
x += distance;
} else if (choice == 1) {
x -= distance;
} else if (choice == 2) {
y += distance;
} else {
y -= distance;
}
}
}
Walker w;
void setup() {
size( 640, 360 );
w = new Walker( new Random() );
background(255);
}
void draw() {
w.step();
w.display();
}
I wanted to avoid globals and I like tinkering with syntax whilst I learn, so I pass in a new Random into the Walker() constructor and set an internal generator property point to it. In the Walker’s draw() function, I create a Gaussian random number and also the uniform random number used to pick a direction (as in earlier examples). To get the distance I picked a mean step size of 10 and a standard deviation of 3. I’ve no idea how “right” that is, but it seemed like a useful set of numbers. I guessed that the canvas would be better larger, to accomodate the leaping around, so I increased it in the setup().
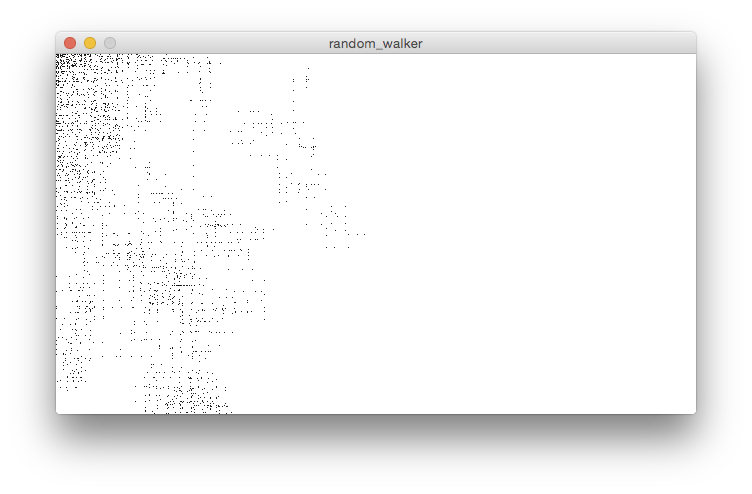
The mesh pattern is quite pleasing. The scattered dots give off the feeling of a malevolent cloud, looming and bifuricating.
It’s not what I was expecting; the earlier examples would draw a trail, and I think that should continue here. The reason the earlier examples drew a trail was that they all had a step size of 1, placing each new step next to the previous one. The new walker still creates a trail (in that each new point is chosen relative to the previous), but doesn’t draw it.
A tangle of boxes
Here’s an implementation that draws lines between the points.
import java.util.Random;
class Walker {
int prev_x;
int prev_y;
Random generator;
Walker( Random gen ) {
prev_x = width/2;
prev_y = height/2;
generator = gen;
}
void walk() {
float stepSize = (float) generator.nextGaussian();
int choice = int(random(4));
int mean = 10;
int sd = 3;
float new_x;
float new_y;
float distance = sd * stepSize + mean;
if (choice == 0) {
new_x = prev_x + distance;
new_y = (float) prev_y;
} else if (choice == 1) {
new_x = prev_x - distance;
new_y = (float) prev_y;
} else if (choice == 2) {
new_y = prev_y + distance;
new_x = (float) prev_x;
} else {
new_y = prev_y - distance;
new_x = (float) prev_x;
}
stroke(0);
line(prev_x, prev_y, new_x, new_y );
prev_x = (int) new_x;
prev_y = (int) new_y;
}
}
Walker w;
void setup() {
size( 640, 360 );
w = new Walker( new Random() );
background(255);
}
void draw() {
w.walk();
}
The previous examples used a separate function to “step” the coordinates of the walker. I didn’t want to add “next x” and “next y” variables to the class, because they don’t need to persist after the draw() method, but they do need to be used with the previous x and y values, so I merged the stepping and drawing into a single walk() function. This is convenient, but dilutes the single-responsibility principle a little.
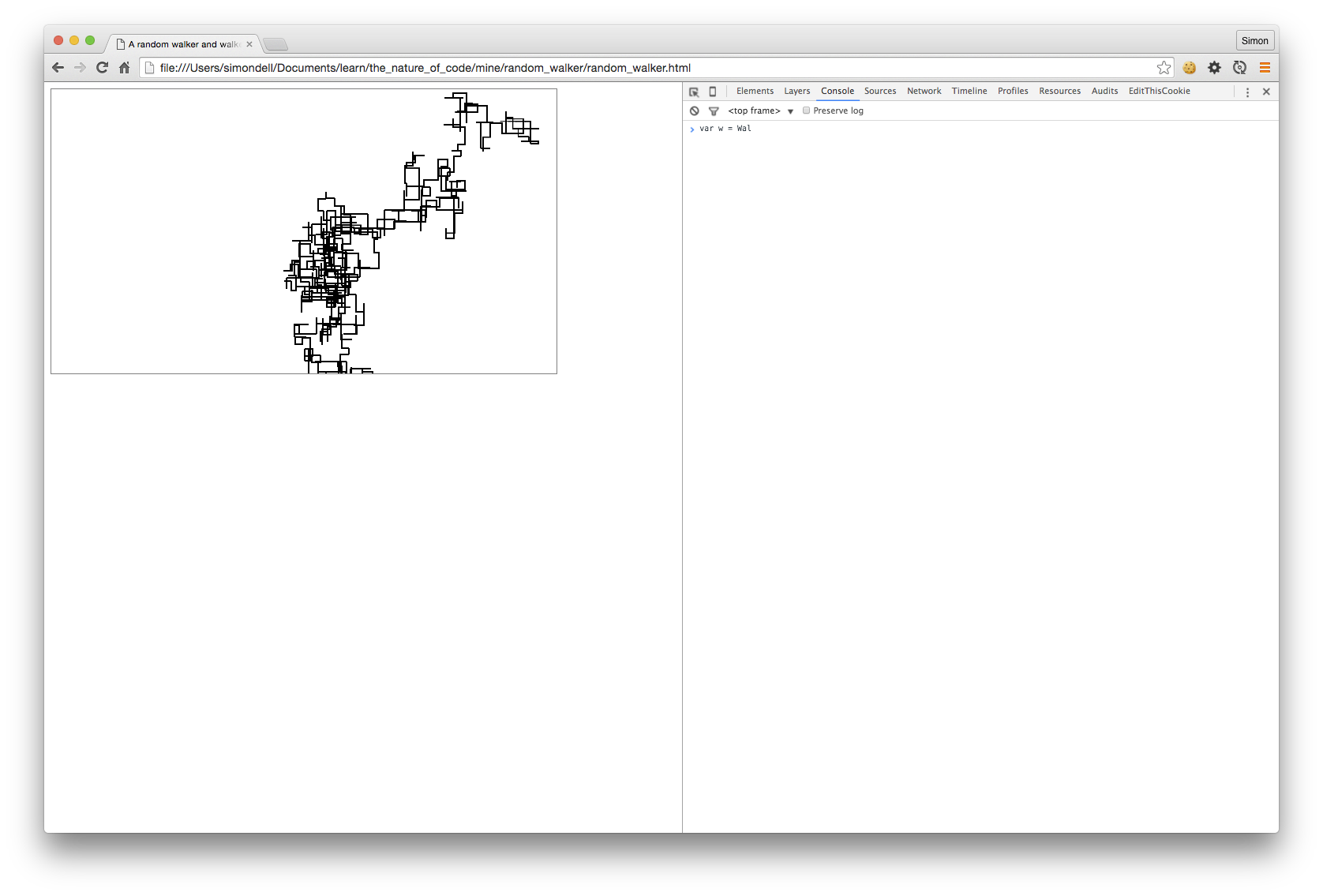
This version draws out a kind of erratic grid pattern: a derranged goblin with Etch-o-sketch, manic digital girders.

In JavaScript
It was good seeing both the dot and line patterns in the Processing implementations so I’ll recreate both in JavaScript.
Dots
Firstly, the application will need the Random.js library used in the previous exercise. I also decided to move the Frames definition outside of the HTML file. In theory, this will make it easier to import into other projects. For now I’ve only moved it as far as a separate file in the same directory, so it wont help much in that regard yet.
<script src="random-0.26.js"></script>
<script src="frames.js"></script>
I worked out how to get around the minor code design issue I had with the Processing implementation, regarding keeping the step() function. I liked that function, even if it wasn’t neccessary. Instead of removing it, I had it update a stepSize property on the Walker. The draw() function still does most of the work, as in the Processing version.
(function( Frames, Random ){
var canvasWidth = 640;
var canvasHeight = 360;
var context = null;
// A Walker "class"
function Walker(context, x, y) {
this.context = context;
this.x = x;
this.y = y;
this.stepSize = 0;
}
Walker.prototype.step = function () {
var sigma = 3;
var mu = 10;
this.stepSize = Random.normal( mu, sigma );
return this;
}
Walker.prototype.display = function () {
var choice = parseInt( Math.random() * 4, 10 );
var new_x, new_y;
switch( choice ) {
case 0:
new_x = this.x + this.stepSize;
new_y = this.y;
break;
case 1:
new_x = this.x - this.stepSize;
new_y = this.y;
break;
case 2:
new_x = this.x;
new_y = this.y + this.stepSize;
break;
case 3:
new_x = this.x;
new_y = this.y - this.stepSize;
break;
}
this.context.fillStyle = 'rgb(0,0,0)';
this.context.fillRect( new_x, new_y, 1, 1 );
this.x = new_x;
this.y = new_y;
return this;
}
function setup () {
context = Frames.setupCanvas( canvasWidth, canvasHeight );
walker = new Walker( context, context.canvas.width / 2, context.canvas.height / 2 );
}
function draw () {
walker.step().display();
}
Frames.go( setup, draw );
})( Frames, new Random() );
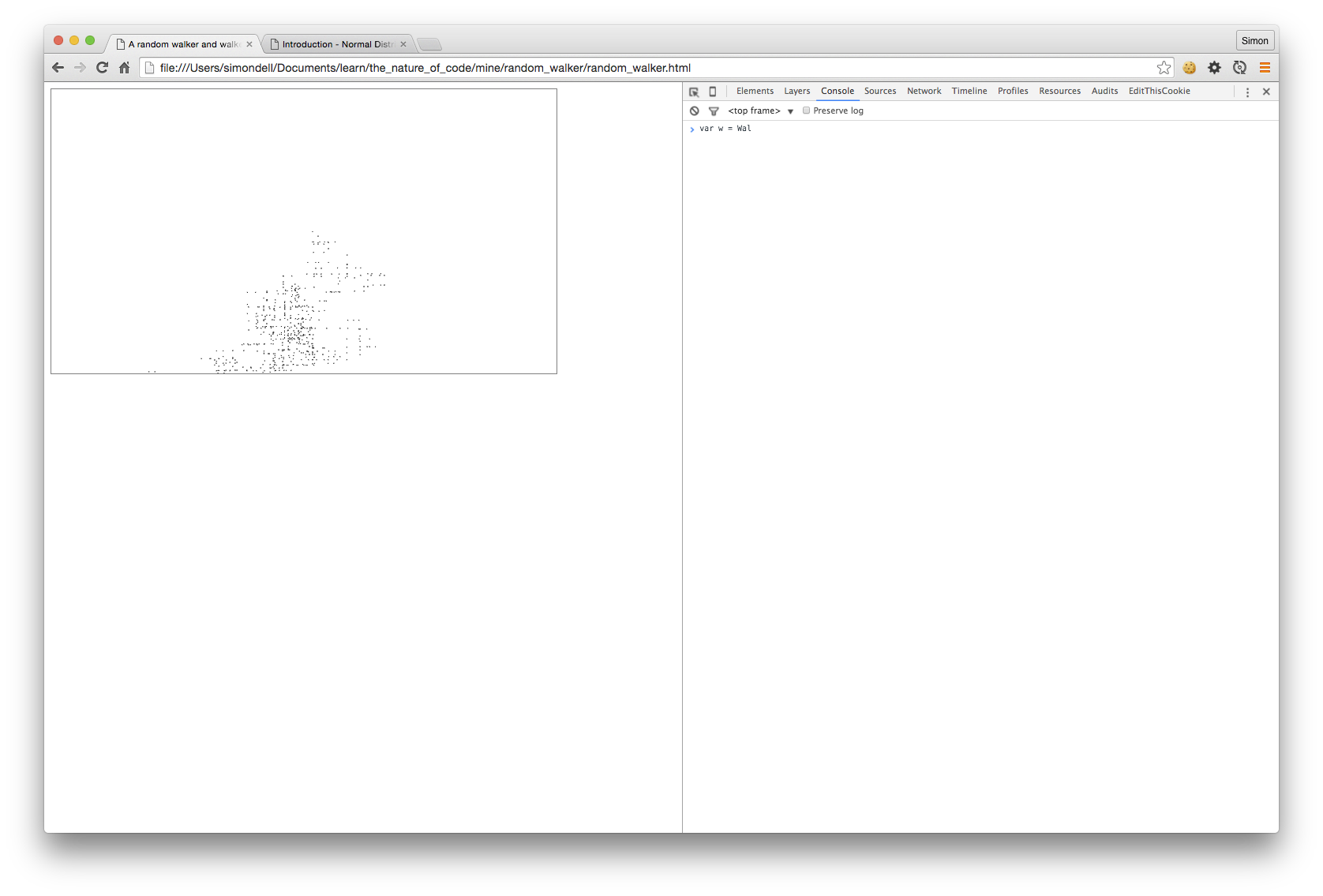
Boxes
This is just like the previous one, but with a draw() function which draws lines from the previous point to the current one.
(function( Frames, Random ){
var canvasWidth = 640;
var canvasHeight = 360;
var context = null;
// A Walker "class"
function Walker(context, x, y) {
this.context = context;
this.x = x;
this.y = y;
this.stepSize = 0;
}
Walker.prototype.step = function () {
var sigma = 3;
var mu = 10;
this.stepSize = Random.normal( mu, sigma );
return this;
}
Walker.prototype.display = function () {
var choice = parseInt( Math.random() * 4, 10 );
var new_x, new_y;
switch( choice ) {
case 0:
new_x = this.x + this.stepSize;
new_y = this.y;
break;
case 1:
new_x = this.x - this.stepSize;
new_y = this.y;
break;
case 2:
new_x = this.x;
new_y = this.y + this.stepSize;
break;
case 3:
new_x = this.x;
new_y = this.y - this.stepSize;
break;
}
this.context.lineWidth = 1;
this.context.strokeStyle = 'rgb(0,0,0)';
this.context.lineTo( new_x, new_y );
this.context.stroke();
this.x = new_x;
this.y = new_y;
return this;
}
function setup () {
context = Frames.setupCanvas( canvasWidth, canvasHeight );
walker = new Walker( context, context.canvas.width / 2, context.canvas.height / 2 );
}
function draw () {
walker.step().display();
}
Frames.go( setup, draw );
})( Frames, new Random() );
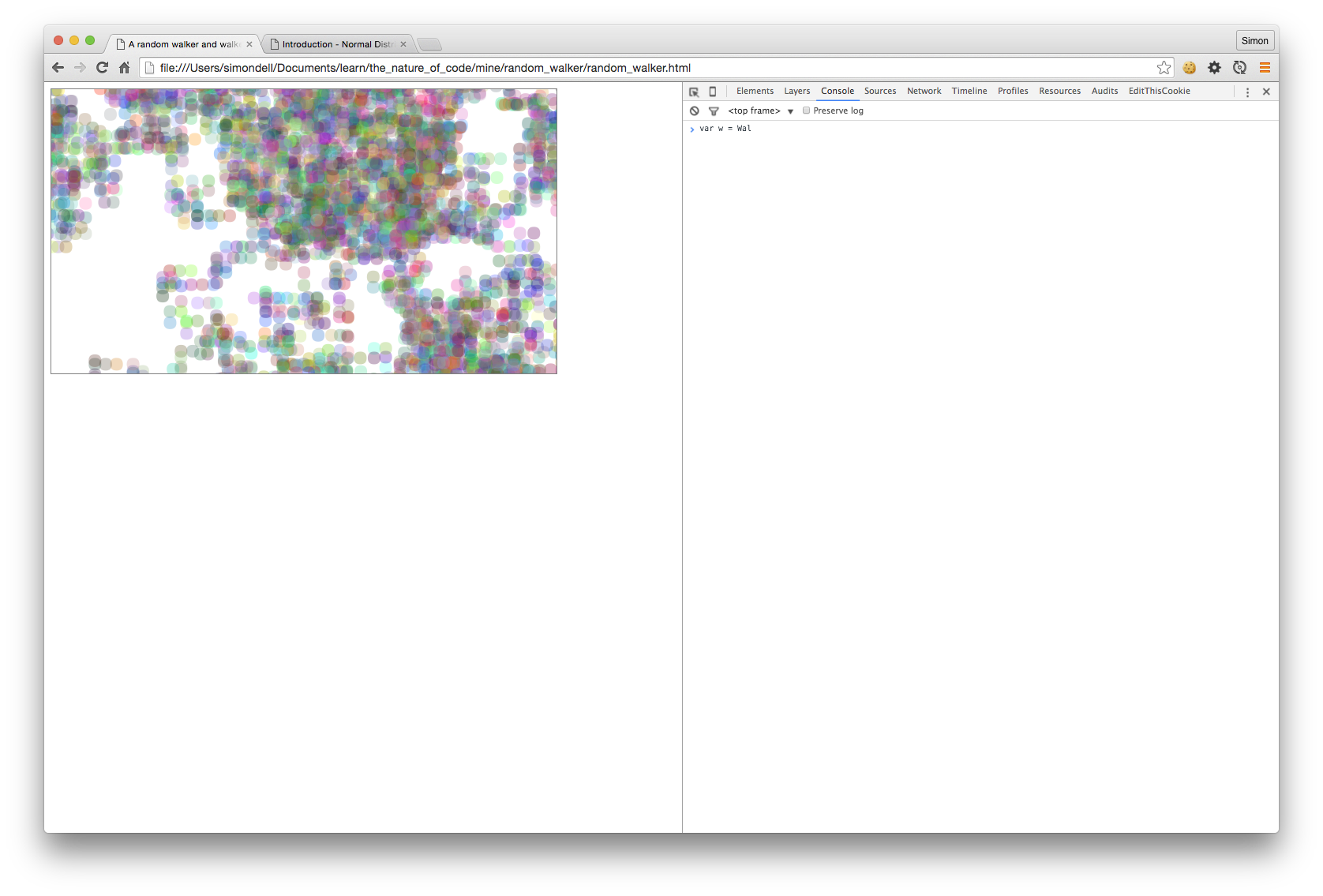
All the colours
The cloudy patterns produced by the “dots” version were quite appealing. I thought it might be nice to have an autonomous paint splatter - like the “dots” crossed with the paint splatter from the earlier exercise.
In JavaScript
(function( Frames, Random ){
var canvasWidth = 640;
var canvasHeight = 360;
var context = null;
// A Walker "class"
function Walker(context, x, y) {
this.context = context;
this.x = x;
this.y = y;
this.stepSize = 0;
}
Walker.prototype.step = function () {
var sigma = 4;
var mu = 15;
this.stepSize = Random.normal( mu, sigma );
return this;
}
Walker.prototype.display = function () {
var red = parseInt( Random.normal( 125, 70 ), 10 );
var green = parseInt( Random.normal( 125, 70 ), 10 );
var blue = parseInt( Random.normal( 125, 70 ), 10 );
var choice = parseInt( Math.random() * 4, 10 );
var new_x, new_y;
switch( choice ) {
case 0:
new_x = this.x + this.stepSize;
new_y = this.y;
break;
case 1:
new_x = this.x - this.stepSize;
new_y = this.y;
break;
case 2:
new_x = this.x;
new_y = this.y + this.stepSize;
break;
case 3:
new_x = this.x;
new_y = this.y - this.stepSize;
break;
}
this.context.fillStyle = 'rgba('+ red +','+ green +','+ blue +',0.3 )';
this.context.beginPath();
this.context.arc( new_x, new_y, 8, 0, 2 * Math.PI );
this.context.fill();
this.x = new_x;
this.y = new_y;
return this;
}
function setup () {
context = Frames.setupCanvas( canvasWidth, canvasHeight );
walker = new Walker( context, context.canvas.width / 2, context.canvas.height / 2 );
}
function draw () {
walker.step().display();
}
Frames.go( setup, draw );
})( Frames, new Random() );
Starting with the “dots” version, above, I tweaked things a little. I copyed the circle drawing commands from the spray gun exercise, tinkered with the mean and standard deviation until I found a feel for the dot drawings that I was happy with. I wanted a bit more space between the dots, but when I set the mean to a higher value (20), the trails had a tendancy to move off the canvas too quickly, and take too long to come back on again.
In Processing
import java.util.Random;
class Walker {
int x;
int y;
Random generator;
Walker( Random gen ) {
x = width/2;
y = height/2;
generator = gen;
}
void display() {
float red, green, blue;
red = (float) generator.nextGaussian() * 125 + 60;
green = (float) generator.nextGaussian() * 125 + 60;
blue = (float) generator.nextGaussian() * 125 + 60;
noStroke();
fill((int)red, (int)green, (int)blue, 30);
ellipse(x,y, 8, 8);
}
void step() {
float stepSize = (float) generator.nextGaussian();
int choice = int(random(4));
int mean = 10;
int sd = 5;
float distance = sd * stepSize + mean;
if (choice == 0) {
x += distance;
} else if (choice == 1) {
x -= distance;
} else if (choice == 2) {
y += distance;
} else {
y -= distance;
}
}
}
Walker w;
void setup() {
size( 640, 360 );
w = new Walker( new Random() );
background(255);
}
void draw() {
w.step();
w.display();
}
Picking the colours, in a gaussian way, in the draw() function.
